EXERCÍCIOS EXTRAS - resolvidos

01. (OBM) Esmeralda tem uma garrafa com 9 litros de uma mistura que tem 50% de álcool e 50% de água. Ela quer colocar água na garrafa de tal forma que apenas 30% da mistura seja de álcool. Quantos litros de água ela irá colocar?

02. (OBM) Se a, b, c e d são, em alguma ordem, 1, 2, 3 e 4. Qual é o maior valor possível de   ab + bc + cd + da?

03. (OBM) Dizemos que dois ou mais números, com a mesma quantidade de algarismos, são membros da mesma família, quando todos possuem pelo menos um algarismo em comum. Por exemplo, os números 32, 25 e 22 pertencem à mesma família, enquanto que 123, 245 e 568 não pertencem à mesma família, pois 123 e 568 não pertencem à mesma família. Qual é a maior quantidade de membros de uma família, cujos elementos têm três algarismos?

04. (OBM) Determine a quantidade de inteiros de dois algarismos que são divisíveis pelos seus algarismos.

05. (OBM) Na figura abaixo, ABCD e EFGH são quadrados de lado 48 cm. Sabendo que A é o ponto médio de EF e G é o ponto médio de DC, determine a área destacada em cm².

06. (Teláris – Pag.176 – ex.34)  O ∆ABC determina uma região plana com área de 120 cm².  O ∆DEC determina uma região plana com área de 270 cm².  Calcule AB, CD e DE, sabendo que ∆ABC ≈ ∆DEC.

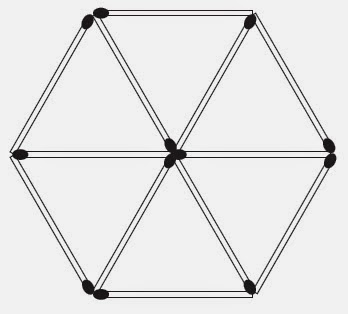
07. (OBM) Usando palitos de fósforos, podemos construir um hexágono regular, formado por seis triângulos equiláteros unitários, como mostra a figura. Juntando mais palitos a esse hexágono, queremos obter outro hexágono regular com o quádruplo da área, também formado por triângulos equiláteros unitários. Quantos palitos deverão ser acrescentados?

A) 12   B) 24   C) 30  D) 36   E) 48    

08. (OBM) O relógio de parede indica inicialmente meio-dia.

Os ponteiros das horas e dos minutos irão formar um ângulo de 90 graus pela primeira vez:

A) entre 12h e 12h10min.

B) entre 12h10min e 12h15min.

C) entre 12h15min e 12h20min.

D) entre 12h20min e 12h25min.

E) após as 12h25min.

09. (OBM) Na figura abaixo, ABCDE é um pentágono regular, CDFG é um quadrado e DFH é um triângulo equilátero.  O valor do ângulo β é:

A) 30º       B) 36º      C) 39º       D) 45º    E) 60º

10. (Teláris-Mat9-Pág205-Ex.11, UniMontes-MG).  O quadrado MNPQ está inscrito no triângulo ABC. A área do triângulo PBQ assinalado na figura abaixo é:

a) 16    b) 18    c) 12    d) 14

Soluções:

Ex.01-Solução) 

Ex.02-Solução)

ab + bc + cd + da =  b(a+c) + d(a+c) = (a+c).(b+d)

Se a=1, então:

[a,c] = [1,2], [1,3], [1,4]

[b,d] = [3,4], [2,4], [2,3]

Logo, os possíveis produtos de (a+c).(b+d) são, respectivamente,

3.7 = 21;  4.6 = 24;  5.5 = 25

Portanto, o maior valor é 25

Ex.03-Solução)

Princípio Fundamental da Contagem

O princípio fundamental da contagem diz que um evento que ocorre em n situações independentes e sucessivas, tendo a primeira situação ocorrendo de m₁ maneiras, a segunda situação ocorrendo de m₂ maneiras e assim sucessivamente até a n-ésima situação ocorrendo de m_n maneiras, temos que o número total de ocorrências será dado pelo produto: 

m₁.m₂.m₃. .... .m_n

Solução:

Vamos contar quantos números de três algarismos que não contêm um algarismo “a” fixado e não nulo.

Assim temos:

a) 8 escolhas para o algarismo das centenas (não pode ser 0 ou a),

b) 9 escolhas para o algarismo das dezenas (não pode ser a),

c) 9 escolhas para os algarismos das unidades (não pode ser a).

Logo, pelo Princípio Fundamental da Contagem:

Há 8.9.9 = 648 números que não possuem o algarismo a.

Assim, como existem 900 números de 3 algarismos:

Existem 900 – 648 = 252 números que possuem o algarismo a ( a ≠ 0 ).

Essa é a maior quantidade de membros que uma família pode ter.

Ex.04-Solução)

Seja genericamente um número de 2 algarismos: n=10x + y

O algarismo y deve ser divisor de n, portanto, temos que: 

n/y = 10x/y + y/y  e y ≠ 0.

Se y ≠ 0 → y/y é sempre inteiro e para que n seja inteiro, deveremos ter 10x/y inteiro, também.  Isso ocorre se e somente se, 10x é múltiplo de y.

E, analogamente, y/x deve ser inteiro também, isto é, y é múltiplo de x.

Ex.05-Solução)

A área hachurada é igual à área do quadrado ABCD subtraído de soma das áreas dos triângulos AFK e AEL.

Por simetria temos que: ∆AFK ≡ ∆DGK, então

Como ponto A é médio de FE, então AF = 24 cm.

∆AFK é retângulo em F, portanto podemos aplicar o teorema de Pitágoras:

x² = 24² + (48-x)² → x² = 24² + 48² - 2.48.x + x² →

0 = 2.12.24 + 48.48 – 2.48.x → 12.48 + 48.48 – 2.48.x = 0 →

12 + 48 – 2.x = 0 → 60 – 2.x = 0 → x = 30

Os triângulos ∆AFK e ∆AEL são semelhantes, portanto, é verdade que:

AF/EL = FK/AE → 24/EL = (48-30)/24 → 24/EL = 18/24 → 24/EL = 3/4 

→ EL = 24.4/3 = 32  → EL = 32 cm

A área do ∆AFK = 1/2.18.24 = 216 cm²

A área do ∆AEL = 1/2.24.32 = 384 cm²

A área do □ABCD = 48.48 = 2304 cm²

Portanto, a área da parte hachurada:  A = 2304 –(216+384) = 1704 cm²

 A = 1704 cm²

Ex.06-Solução)

Como ∆ABC ≈ ∆DEC (= semelhantes):

(3y – 3)/4y = (z + 11)/(4x – 1) → 12xy – 12x – 3y + 3 = 4yz + 44y →

12xy – 12x + 3 = 4yz + 47y → 12xy – 12x - 4yz  - 47y + 3 = 0    (Eq-1)

Área do ∆ABC = 1/2.x.(3y-3) = 270 → 3xy – 3x = 2.120 →

12xy – 12x = 4.2.120  (Eq-2)

Área do ∆DEC = 1/2.z.4y = 270 → 4yz = 2. 270 (Eq-3)

Reescrevendo a Eq-1, temos:

(12xy – 12x) - 4yz  - 47y + 3 = 0   e substituindo os termos com as Eq-2 e Eq-3:

4.2.120 – 2.270 – 47y + 3 = 0 → - 47y = 2.270 – 4.2.120 – 3 → y = 9

Eq-3:  4yz = 2.270 → 4.9.z = 2.270 → z = 15

Eq-2: 12xy – 12x = 4.2.120 → 12x.9 – 12x = 4.2.120 → 8x = 80 → x = 10

Portanto:

AB = x = 10 cm

CD = 4y = 4.9 = 36 cm

DE = z = 15 cm

OUTRA MANEIRA DE RESOLVER

Mais elegante e inteligente de resolver a questão:

Como ∆ABC ≈ ∆DEC e foram dadas as respectivas áreas 120 e 270, sabemos que a raiz quadrada da proporção entre áreas é igual às relações entre os lados dos triângulos.

Vamos determinar o valor de y:

(3y – 3)/4y = 2/3 → 3.(3y – 3) = 2.4y → 9y – 9 = 8y → y = 9

Determinando os valores de x e z:

x/z = 2/3 → 3x = 2z → 9x = 6z (eq-1)

(z + 11)/(4x – 1) = 2/3 → 3z +33 = 8x – 2 → 6z + 66 = 16x – 4 (eq-2)

(eq-1) em (eq-2):

9x + 66 = 16x – 4 → 7x = 70 → x = 10 

3x = 2z → 2z = 30 → z = 15

Logo:

AB = x = 10 cm

CD = 4y = 4.9 = 36 cm

DE = z = 15 cm

Ex.07-Solução)

Outro hexágono possui 4 vezes a área do primeiro.  Isto é, o lado do hexágono deve ser 2 vezes maior.

Sendo um triângulo unitário:

Temos:

Em azul e vermelho os palitos necessários.  São 30 palitos.

Portanto, a resposta é a alternativa “c”.

Ex.08-Solução)

Por ser questão de múltipla alternativa, portanto, utilizando a intuição podemos chegar à alternativa certa: 

Enquanto o ponteiro maior anda 90º o ponteiro pequeno de horas anda 7,5 graus, portanto: o ponteiro grande forma um ângulo de 90º com o ponteiro pequeno, quando o ponteiro grande andou (90 + α)º e α é inferior a 30º, então a alternativa correta é “c”.

Agora vamos calcular:

Enquanto o ponteiro grande (minutos) anda 360º o ponteiro pequeno (horas) anda 30º, na mesma proporção: grande anda 90º, o pequeno anda 7,5º.  Então, genericamente, quando o grande anda β graus, o pequeno anda de α graus. 

O que precisamos encontrar é: β – α = 90º

Podemos escrever a seguinte relação:

360/30 = β/α   → 12 = β/α   → β = 12α

β – α = 90º   ↔  12α – α = 90  ↔ 11α = 90  ↔ α ≈ 8,18 º

Logo:  β = 12α  ↔ β ≈ 12.8,18 = 98,16 ↔ β ≈ 98,16º

Para ponteiro grande:

90º = 15 minutos, então para 98,16 = x

Logo:  15/90 = x/98,16  → x ≈ 16,37 min → x ≈ 16min 21s

O ponteiro grande e ponteiro pequeno formam ângulo de 90º, pela primeira vez, após 12:00:00h é:

Resultado:   ≈ 12h 16min 21s

Ex.09-Solução, alternativa-c)

Pela figura podemos concluir que o triângulo EDH é isósceles.

Vamos calcular o ângulo EDH do triângulo EDH:  a soma dos ângulos no ponto D é igual a 360º.

Ângulo EDC do pentágono regular = (5-2)/5 * 180 = 108º

Ângulo CDF do quadrado regular = 90º

Ângulo FDH do triângulo eqüilátero = 60º

Ângulo EDH do triângulo isósceles = 360 – 108 – 90 – 60 = 102º

Sabemos que a soma dos ângulos internos de um triângulo é 180º.

Então no triângulo isósceles EDH: 2β + 102 = 180º

Logo: β = 39

Ex.10-Solução, alternativa - a)

Podemos notar que os 3 triângulos retângulos são todos semelhantes entre si.

Isto é: ∆PBQ ≈ ∆AMN ≈ ∆CNP

Portanto, temos: